October 2018

This post aims to explain mathematically how populations change.

Our first attempt is based on ideas put forward by Thomas Malthus’ article “An Essay on the Principle of Population” published in 1798.

Let $p(t)$ denotes total population at time $t$ .

Assume in a small interval $\Delta t$ , births and deaths are proportional to $p(t)$ and $\Delta t$ . i.e.

births = $a \cdot p(t) \Delta t$

deaths = $b \cdot p(t) \Delta t$

where $a, b$ are constants.

It follows that the change of total population during time interval $\Delta t$ is

$p(t+\Delta t) - p(t) = a\cdot p(t)\Delta t - b \cdot p(t)\Delta t = r\cdot p(t)\Delta t$

where $r = a - b$ .

Dividing by $\Delta t$ and taking the limit as $\Delta t \rightarrow 0$ , we have

$\lim\limits_{\Delta \rightarrow 0} {p(t+\Delta t) - p(t) \over \Delta t} = r \cdot p(t)$

which is

${d \over dt} p(t) = r \cdot p(t)\quad\quad\quad(1)$

a first order differential equation.

Since (1) can be written as

${1 \over p(t)} {d \over dt} p(t) = r$ ,

integrate with respect to $t$ ; i.e.

$\int {1 \over p(t)}{d \over dt} p(t)dt = \int {r} dt$

leads to

$\log p(t) = r\cdot t + c$

where $c$ is the constant of integration.

If at $t=0, p(0) = p_0$ , we have

$c = \log p_0$

and so

$p(t) = p_0 e^{r\cdot t}\quad\quad\quad(2)$

The result of our first attempt shows that the behavior of the population depends on the sign of constant $r$ . We have exponential growth if $r > 0$ , exponential decay if $r < 0$ and no change if $r = 0$ .

The world population has been on a upward trend ever since such data is collected (see “World Population by Year“)

Qualitatively, our model (2) with $r>0$ indicates this trend. However, it also predicts the world population would grow exponentially without limit. And that, is most unlikely to occur, since there are so many limitation factors to growth: lack of food, insufficient energy, overcrowding, disease and war.

Therefore, it is doubtful that model (1) is The One.

Our second attempt makes a modification to (1). It takes the limitation factors into consideration by replacing constant $r$ in (1) with a function $r(t)$ . Namely,

$r(t) = \gamma - \alpha \cdot p(t)\quad\quad\quad(3)$

where $\gamma$ and $\alpha$ are both positive constants.

Replace $r$ in (1) with (3),

${d \over dt} p(t) = (\gamma - \alpha \cdot p(t)) p(t) = \gamma (1 - {p(t) \over {\gamma \over \alpha}}) p(t)\quad\quad\quad(4)$

Since $r(t)$ is a monotonic decreasing function, it shows as population grows, the growth slows down due to the limitation factors.

Let $p_{\infty} = {\gamma \over \alpha}$ ,

${d \over dt} p(t) = \gamma (1- {p(t) \over p_{\infty}}) p(t)\quad\quad\quad(5)$

This is the Logistic Differential Equation.

Written differently as

${d \over dt} p(t) - \gamma \cdot p(t) = -{\gamma \over p_{\infty}} p(t)^2$ ,

the Logistic Differential Equation is also a Bernoulli’s equation (see “Meeting Mr. Bernoulli“)

Let’s understand (5) geometrically without solving it.

Two constant functions, $p(t) = 0$ or $p_{\infty}$ are solutions of (5), since

${d \over dt} 0 = \gamma (1-{0\over p_{\infty}}) 0 = 0$

and

${d \over dt} p_{\infty} = \gamma (1-{p_{\infty} \over {p_{\infty}}}) p_{\infty} = 0$ .

Plot $p(t)$ vs. ${d \over dt} p(t)$ in Fig. 1, the points, $0$ and $p_{\infty}$ , are where the curve of ${d \over dt} p(t)$ intersects the axis of $p(t)$ .

Screen Shot 2018-10-23 at 9.42.20 AM.png

Fig. 1

At point $A$ where $p(t) > p_{\infty}$ , since ${d \over dt} p(t) < 0$ , $p(t)$ will decrease; i.e., $A$ moves left toward $p_{\infty}$ .

Similarly, at point $B$ where $p(t) < p_{\infty}, {d \over dt} p(t) > 0$ implies that $p(t)$ will increase and $B$ moves right toward $p_{\infty}$ .

The model equation can also tell the manner in which $p(t)$ approaches $p_{\infty}$ .

Let $p = p(t)$ ,

${d^2 \over dt^2} p(t) = {d \over dt}({d \over dt} p)$

$= {d \over dp} ({d \over dt}p) \cdot {d \over dt} p$

$= {d \over d p}(\gamma (1-{p \over p_{\infty}})p)\cdot {d \over dt }p$

$= \gamma(1 - {2 p\over p_{\infty}})\cdot \gamma (1-{p \over p_{\infty}})p$

$= \gamma^2 p ({{2 p} \over p_{\infty}} -1)({p \over p_{\infty}}-1)$

As an equation with unknown $p$ , $\gamma^2 p ({{2 p} \over p_{\infty}} -1)({p \over p_{\infty}}-1)=0$ has three zeros:

$0, {p_{\infty} \over 2}$ and $p_{\infty}$ .

Therefore,

${d^2 \over dt^2}p > 0$ if $p > p_{\infty}$ ,

${d^2 \over dt^2} p < 0$ if ${p_{\infty} \over 2} < p < p_{\infty}$

and

${d^2 \over dt^2} p > 0$ if $p < {p_{\infty} \over 2}$ .

Consequently $p(t)$ , the solution of initial-value problem

$\begin{cases} {d \over dt} p(t) = \gamma (1-{p(t) \over p_{\infty}}) p(t) \\ p(0)=p_0 \end{cases}\quad\quad(6)$

where $p_0 \neq 0, p_{\infty}$ behaves in the manner illustrated in Fig. 2.

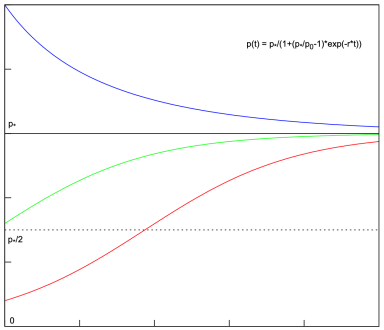
Screen Shot 2018-10-23 at 9.50.25 AM.png

Fig. 2

If $p_0 > p_{\infty}, p(t)$ approaches $p_{\infty}$ on a concave curve. Otherwise, when ${p_{\infty} \over 2} \leq p_0 < p_{\infty}, p(t)$ moves along a convex curve. For $p_0 < {p_{\infty} \over 2}$ , the curve is concave first. It turns convex after $p(t)$ reaches ${p_{\infty} \over 2}$ .

Next, let’s solve the initial-value problem analytically for $p_0 \neq 0, p_{\infty}$ .

Instead of using the result from “Meeting Mr. Bernoulli“, we will start from scratch.

At $t$ where $p(t) \neq 0, p_{\infty}$ , we re-write (5) as

${1 \over p(t)(1-{p(t) \over p_{\infty}}) }{d \over dt} p(t) = \gamma$ .

Expressed in partial fraction,

$({1 \over p(t)} + {{1 \over p_{\infty}} \over {1-{p(t) \over p_{\infty}}}}) {d \over dt} p(t) = \gamma$ .

Integrate it with respect to $t$ ,

$\int ({1 \over p(t)} + {{1 \over p_{\infty}} \over {1-{p(t) \over p_{\infty}}}}) {d \over dt} p(t) dt = \int \gamma dt$

gives

$\log p(t) - \log (1-{p(t) \over p_{\infty}}) = \gamma t + c$

where $c$ is the constant of integration.

i.e.,

$\log {p(t) \over {1-{p(t) \over p_{\infty}}}} = \gamma t + c$ .

Since $p(0) = p_0$ , we have

$c = {\log {p_{0} \over {1-{p_0 \over p_{\infty}}}}}$

and so

$\log ({{p(t) \over {1-{p(t) \over p_{\infty}}}} \cdot {{1-{p_0 \over p_{\infty}}}\over p_0}} )=\gamma t$ .

Hence,

${{p(t) \over {1 - {p(t) \over p_\infty}}}= {{p_0 \cdot e^{\gamma t}} \over {1-{p_0 \over p_\infty}}}}$ .

Solving for $p(t)$ gives

$p(t) = { p_{\infty} \over {1+({p_{\infty} \over p_0}-1)e^{-\gamma \cdot t}}}\quad\quad\quad(7)$

We proceed to show that (7) expresses the value of $p(t)$ , the solution to (6) where $p_0 \neq 0, p_{\infty}$ , for all $t$ ‘s (see Fig.3)

Screen Shot 2018-10-25 at 4.29.47 PM.png

Fig. 3

From (7), we have

$\lim\limits_{t \rightarrow \infty} p(t) = p_{\infty}$ .

It validates Fig. 1.

(7) also indicates that none of the curves in Fig. 2 touch horizontal line $p(t) = p_{\infty}$ .

If this is not the case, then there exists at least one instance of $t$ where $p(t) = p_{\infty}$ ; i.e.,

${p_{\infty} \over {1+({p_{\infty} \over p_0}-1)e^{-\gamma \cdot t}}} = p_{\infty}$ .

It follows that

${({p_{\infty} \over {p_0}} - 1) e^{-\gamma t}} = 0$

Since ${e^{-\gamma t}} > 0$ (see “Two Peas in a Pod, Part 2“), it must be true that

$p_0 = p_{\infty}$ .

But this contradicts the fact that (7) is the solution of the initial-value problem (6) where $p_0 \neq 0,p_\infty$ .

Reflected in Fig.1 is that $A$ and $B$ will not become $p_{\infty}$ . They only move ever closer to it.

Last, but not the least,

${\lim \limits_{t \rightarrow \infty}} {d \over dt} p(t) = \gamma (1-{{ \lim\limits_{t \rightarrow \infty} p(t)} \over p_{\infty}}) {\lim\limits_{t \rightarrow \infty} p(t)} = \gamma (1 - {p_{\infty} \over p_{\infty}}) p_{\infty} = 0$ .

Hence the title of this post.

220px-Wolfram_Language_Logo_2016.svg.png

You see things; and you say “Why?”

But I dream things that never were; and I say “Why not?”

George Bernard Shaw in Back to Methuselah

The Wolfram Language function DSolve and NDSolve can solve differential equations.

Let’s look at a few examples.

Example 1 Solving an ODE symbolically. The solution, a function, is evaluated at a given point.

Screen Shot 2018-10-06 at 8.55.21 PM.png

Example 2 Solving an ODE symbolically. Redefine a function and evaluate it at a given point.

Screen Shot 2018-10-06 at 8.52.38 PM.png

Example 3 Solving an ODE initial-value problem symbolically. Get the value at a given point from the symbolic solution.

Screen Shot 2018-10-06 at 8.44.42 PM.png

Example 4 Solving an ODE initial-value problem numerically. Get the value at a given point from the numerical solution.

Screen Shot 2018-10-06 at 8.57.59 PM.png

Regarding whether to specify ‘y‘ or ‘y[x]‘ in DSolve, the only decent explanation I can find is in Stephen Wolfram’s book “The Mathematica Book”. This is straight from horse’s mouth:

“When you ask DSolve to get you a solution for y[x], the rule it returns specify how to replace y[x] in any expression. However, these rules do not specify how to replace objects such as y'[x]. If you want to manipulate solutions that you get from DSolve, you will often find it better to ask for solutions for y, rather than y[x].”

He then proceeds to give an illustration:

Screen Shot 2018-10-07 at 12.30.46 AM.png

Had you started with DSolve[y'[x]==x+y[x], y[x], x], the result would be

Screen Shot 2018-10-07 at 12.34.12 AM.png

As expected, only y[x] is replaced.

Month: October 2018

What moves fast, will slow down, Part One

You say, “y” I say, “y[x]”